A directed acyclic graph (DAG) is a good model for processes and structures that have partial orders: You may know that a > c and b > c but may not have information on how a and b compare to each other.
One can always make a total order out of a partial order. This is what topological sort does. A topological sort of a DAG is a linear ordering of vertices such that if (u, v) ∈ E then u appears somewhere before v in the ordering.
Some real world examples include
Here is the book's example ... a hypothetical professor (not me!) getting dressed (what node did they start the search at? Could it have been done differently?):

We can make it a bit more complex, with catcher's outfit (click to compare your answer):
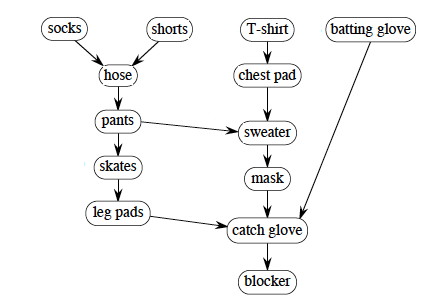
The answer given starts with the batting glove and works left across the unvisted nodes. What if we had started the search with socks and worked right across the top nodes? If you put your clothes on differently, how could you get the desired result? Hint: add an edge.
As noted previously, one could start with any vertex, and once the first tree was constructed continue with any artibrary remaining vertex. It is not necessary to start at the vertices at the top of the diagram. Do you see why?

Time analysis is based on simple use of DFS: Θ(V + E).
Lemma: A directed graph G is acyclic if and only if a DFS of G yields no back edges.
See text for proof, but it's quite intuitive:
⇒ A back edge by definition is returning to where one started, which means it completes a cycle.
⇐ When exploring a cycle the last edge explored will be a return to the vertex by which the cycle was entered, and hence classified a back edge.
Theorem: If G is a DAG then Topological-Sort(G) correctly produces a topological sort of G.
It sufficies to show that
if (u, v) ∈ E then v.f < u.f
because then the linked list ordering by f will respect the graph topology).
When we explore (u, v), what are the colors of u and v?
Given a directed graph G = (V, E), a strongly connected component (SCC) of G is a maximal set of vertices C ⊆ V such that for all u, v ∈ C, there is a path both from u to v and from v to u.
What are the Strongly Connected Components? (Click to see.)

The algorithm uses GT= (V, ET), the transpose of G = (V, E). GT is G with all the edges reversed.
Strongly-Connected-Components (G)
1. Call DFS(G) to compute finishing times u.f for each vertex u ∈ E.
2. Compute GT
3. Call modified DFS(GT) that considers vertices
in order of decreasing u.f from line 1.
4. Output the vertices of each tree in the depth-first forest
formed in line 3 as a separate strongly connected component.
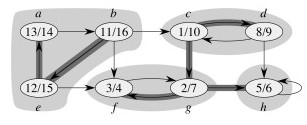
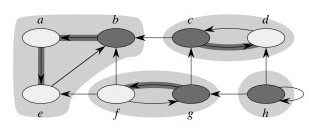
(This is from my own attempt to understand the algorithm. It differs from the book's formal proof.)
G and GT have the same SCC. Proof:
A DFS from any vertex v in a SCC C will reach all vertices in C (by definition of SCC).
So how does the second search on GT help avoid inadvertent inclusion of v' in C?
In the example above, notice how node c corresponds to v and g to v' in the argument above. But we need to also say why nodes like b will never be reached from c in the second search. It is because b finished later in the first search, so was processed earlier and already "consumed" by the correct SCC in the second search, before the search from c could reach it. The following fact is useful in understanding why this would be the case.
Here is GSCC for the above example:
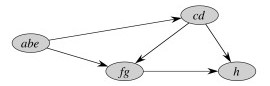
The first pass of the SCC algorithm essentially does a topological sort of the graph GSCC (by doing a topological sort of constituent vertices). The second pass visits the components of GTSCC in topologically sorted order such that each component is searched before any component that can reach that component.
Thus, for example, the component abe is processed first in the second search, and since this second search is of GT (reverse the arrows above) one can't get to cd from abe. When cd is subsequently searched, one can get to abe but it's vertices have already been visited so can't be incorrectly included in cd.
Start at the node indicated by the arrow; conduct a DFS; then click to compare your answer:
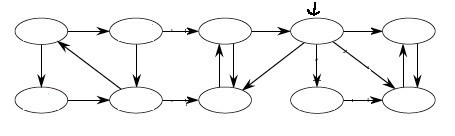
We have provided an informal justification of correctness: please see the CLRS book for a formal proof of correctness for the SCC algorithm.

The CLRS text says we can create GT in Θ(V + E) time using adjacency lists.
The SCC algorithm also has two calls to DFS, and these are Θ(V + E) each.
All other work is constant, so the overall time complexity is Θ(V + E).
An articulation point or cut vertex is a vertex that when removed causes a (strongly) connected component to break into two components.
A bridge is an edge that when removed causes a (strongly) connected component to break into two components.
A biconnected component is a maximal set of edges such that any two edges in the set lie on a common simple cycle. This means that there is no bridge (at least two edges must be removed to disconnect it). This concept is of interest for network robustness.