ICS 311 #5: Quicksort, Probabilistic Analysis and Randomized Algorithms

Outline

1. Quicksort
2. Probabilistic Analysis and Randomized Algorithms
3. Randomized Quicksort
4. Expected Number of Inversions (another example of Probabilistic Analysis)

Readings and Screencasts

• If needed, brush up on probabilities with Appendix C.
• CLRS Sections 5.1-5.3 and Section 7
• Screencasts 10A, 5A, 10B, 5B (also in Laulima and iTunesU)

Quicksort

Motivation

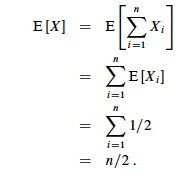
So far we have seen the following sorting algorithms: InsertionSort, MergeSort and HeapSort. We start these Lecture notes with another sorting algorithm: Quicksort. Quicksort, like Mergesort, takes a divide and conquer approach, but on a different basis.

If we have done two comparisons among three keys and find that x < p and p < y, do we ever need to compare x to y? Where do the three belong relative to each other in the sorted array?

Quicksort uses this idea to partition the set of keys to be sorted into those less than the pivot p and those greater than the pivot. (It can be generalized to allow keys equal to the pivot.) It then recurses on the two partitions.

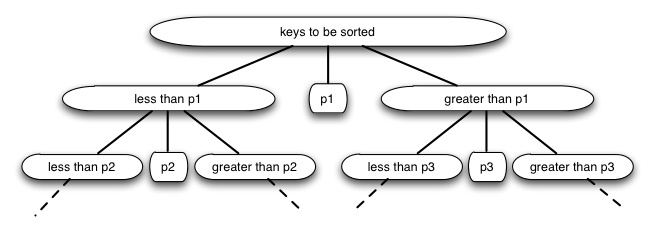
Compare this to Mergesort.

• Both take a recursive divide-and-conquer approach.
• Mergesort does its work on the way back up the recursion tree (merging), while Quicksort does its work on the way down the recursion tree (partitioning).
• Mergesort always partitions in half; for Quicksort the size of the partitions depends on the pivot (this results in Θ(n²) worst case behavior, but expected case remains Θ(n lg n).
• Mergesort requires axillary arrays to copy the data; while as we shall see Quicksort can operate entirely within the given array: it is an in-place sort.

Quicksort performs well in practice, and is one of the most widely used sorts today.

The Quicksort Algorithm

To sort any subarray A[p .. r],   p < r:

Divide:

Partition A[p .. r] into two (possibly empty) subarrays

• A[p .. q-1], where every element is ≤ A[q]
• A[q + 1 .. r], where A[q] ≤ every element

Conquer:

Sort the two subarrays by recursive calls

Combine:

No work is needed to combine: all subarrays (including the entire array) are sorted as soon as recursion ends.

An array is sorted with a call to QUICKSORT(A, 1, A.length):

The work is done in the PARTITION procedure. A[r] will be the pivot. (Note that the end element of the array is taken as the pivot. Given random data, the choice of the position of the pivot is arbitrary; working with an end element simplifies the code):

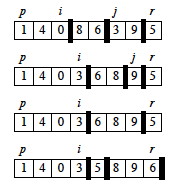
PARTITION maintains four regions.

Three of these are described by the following loop invariants, and the fourth (A[j .. r-1]) consists of elements that not yet been examined:

Loop Invariant:

1. All entries in A[p .. i] are ≤ pivot.
2. All entries in A[i+1 .. j-1] are > pivot.
3. A[r] = pivot.

Example Trace

It is worth taking some time to trace through and explain each step of this example of the PARTITION procedure, paying particular attention to the movement of the dark lines representing partition boundaries.

Continuing ...

Here is the Hungarian Dance version of quicksort, in case that helps to make sense of it!

Correctness

Here use the loop invariant to show correctness:

1. All entries in A[p .. i] are ≤ pivot.
2. All entries in A[i+1 .. j −1] are > pivot.
3. A[r] = pivot.

Initialization:

Before the loop starts, x is assigned the pivot A[r] (satisfying condition 3), and the subarrays a[p .. i] and A[i+1 .. j−1] are empty (trivially satisfying conditions 1 and 2).

Maintenance:

While the loop is running,

• if A[j] ≤ pivot, then i is incremented, A[j] and A[i] are swapped, and j is incremented. Because of the swap, A[i] ≤ x for condition 1. The item swapped into A[j-1] > x by the loop invariant, for condition 2.
• If A[j] > pivot, then j is incremented, sustaining condition 2 (the others are unchanged), as the element added was larger

Termination:

The loop terminates when j=r, so all elements in A are partitioned into one of three cases: A[p .. i] ≤ pivot, A[i+1 .. r-1] > pivot, and A[r] = pivot. The last two lines fix the placement of A[r] by moving it between the two subarrays.

Informal Analysis

The formal analysis will be done on a randomized version of Quicksort (see below). This informal analysis helps to motivate that randomization.

First, PARTITION is Θ(n): We can easily see that its only component that grows with n is the for loop that iterates proportional to the number of elements in the subarray).

The runtime depends on the partitioning of the subarrays:

Worst Case

The worst case occurs when the subarrays are completely unbalanced, i.e., there are 0 elements in one subarray and n-1 elements in the other subarray (the single pivot is not processed in recursive calls). This gives a familiar recurrence (compare to that for insertion sort):

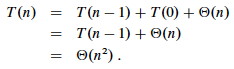
One example of data that leads to this behavior is when the data is already sorted: the pivot is always the maximum element, so we get partitions of size n−1 and 0 each time. Thus, quicksort is O(n²) on sorted data. Insertion sort actually does better on a sorted array! (O(n))

Best Case

The best case occurs when the subarrays are completely balanced (the pivot is the median value): subarrays have about n/2 elements. The reucurrence is also familiar (compare to that for merge sort):

Effect of Unbalanced Partitioning

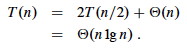
It turns out that expected behavior is closer to the best case than the worst case. Two examples suggest why expected case won't be that bad.

Example: 1-to-9 split

Suppose each call splits the data into 1/10 and 9/10. This is highly unbalanced: won't it result in horrible performance?

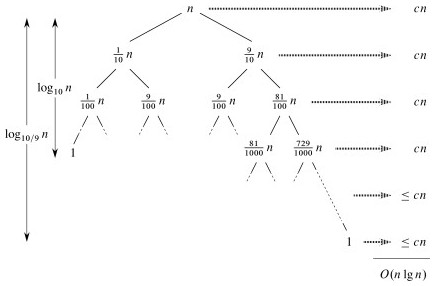
We have log₁₀n full levels and log_10/9n levels that are nonempty.

As long as it's constant, the base of the log does not affect asymptotic results. Any split of constant proportionality will yield a recursion tree of depth Θ(lg n). In particular (using ≈ to indicate truncation of low order digits),

log_10/9n = (log₂n) / (log₂10/9)     by formula 3.15
            ≈ (log₂n) / 0.152
            = 1/0.152 (log₂n)
            ≈ 6.5788 (log₂n)
            = Θ(lg n), where c = 6.5788.

So the recurrence and its solution is:

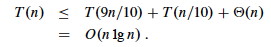
A general lesson that might be taken from this: sometimes, even very unbalanced divide and conquer can be useful.

Example: extreme cases cancel out

With random data there will usually be a mix of good and bad splits throughout the recursion tree.

A mixture of worst case and best case splits is asymptotically the same as best case:

Both these trees have the same two leaves. The extra level on the left hand side only increases the height by a factor of 2, and this constant disappears in the Θ analysis.

Both result in O(n lg n), though with a larger constant for the left.

Probabilistic Analysis

Instead of limiting analysis to best case or worst case, we can analyze all cases based on a distribution of the probability of each case and compute the expected runtime based on this distribution.

We implicitly used probabilistic analysis when we said that given random input it takes n/2 comparisons on average to find an item in a linked list of n items.

Hiring Problem and Cost

To illustrate probabilistic analysis, consider the following problem. Suppose you are using an employment agency to hire an office assistant.

• The agency sends you one candidate per day: interview and decide.
• Cost to interview is c_i per candidate (fee to agency).
• Cost to hire is c_h per candidate (includes firing prior assistant and fee to agency).
• c_h > c_i
• You always hire the best candidate seen so far.

  Hire-Assistant(n)
  1  best = 0                // fictional least qualified candidate
  2  for i = 1 to n
  3    interview candidate i // paying cost  ci
  4    if candidate i is better than candidate best
  5      best = i
  6      hire candidate i    // paying cost ch

What is the cost of this strategy?

• If we interview n candidates and hire m of them, cost is O(c_in + c_hm)
• We interview all n and c_i is small, so we focus on c_hm.
• c_hm varies with each run and depends on interview order
• This is a common paradigm: finding the maximum or minimum in a sequence by examining each element, and changing the winner m times.

Best Case

If each candidate is worse than all who came before, we hire one candidate:
    O(c_in + c_h) = O(c_in)

Worst Case

If each candidate is better than all who came before, we hire all n (m = n):
    O(c_in + c_hn) = O(c_hn) since c_h > c_i
But this is pessimistic. What happens in the average case?

Probabilistic Analysis

• We must know or make assumptions about the distribution of inputs.
• The expected cost is over this distribution.
• The analysis will give us average case running time.

We don't have this information for the Hiring Problem, but suppose we could assume that candidates come in random order. Then the analysis can be done by counting permutations:

• Each ordering of candidates (relative to some reference ordering such as a ranking of the candidates) is equally likely to be any of the n! permutations of the candidates.
• In how many do we hire once? twice? three times? ... n−1 times? n times?
• It depends on how many permutations have zero, one two ... n−2 or n−1 candidates that come before a better candidate.
• This is complicated!
• Instead, we can do this analysis with indicator variables (next section)

Randomized Algorithms

We might not know the distribution of inputs or be able to model it.

Instead we randomize within the algorithm to impose a distribution on the inputs.

An algorithm is randomized if its behavior is determined in parts by values provided by a random number generator.

This requires a change in the hiring problem scenario:

• The employment agency sends us a list of n candidates in advance and lets us choose the interview order.
• We choose randomly.

Thus we take control of the question of whether the input is randomly ordered: we enforce random order, so the average case becomes the expected value.

Probabilistic Analysis with Indicator Random Variables

Here we introduce technique for computing the expected value of a random variable, even when there is dependence between variables. Two informal definitions will get us started:

A random variable (e.g., X) is a variable that takes on any of a range of values according to a probability distribution.

The expected value of a random variable (e.g., E[X]) is the average value we would observe if we sampled the random variable repeatedly.

Indicator Random Variables

Given sample space S and event A in S, define the indicator random variable

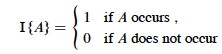
We will see that indicator random variables simplify analysis by letting us work with the probability of the values of a random variable separately.

Lemma 1

For an event A, let X_A = I{A}. Then the expected value E[X_A] = Pr{A} (the probability of event A).

Proof: Let ¬A be the complement of A. Then

E[X_A] = E[I{A}]   (by definition)
    = 1*Pr{A} + 0*Pr{¬A}   (definition of expected value)
    = Pr{A}.

Simple Example

What is the expected number of heads when flipping a fair coin once?

• Sample space S is {H, T}
• Pr{H} = Pr{T} = 1/2
• Define indicator random variable X_H= I{H}, which counts the number of heads in one flip.
• Since Pr{H} = 1/2, Lemma 1 says that E[X_H] = 1/2.

Less Simple Example

What is the expected number of heads when we flip a fair coin n times?

Let X be a random variable for the number of heads in n flips.

We could compute E[X] = ∑_i=0,ni Pr{X=i} -- that is, compute and add the probability of there being 0 heads total, 1 head total, 2 heads total ... n heads total, as is done in C.37 in the appendix and in my screencast lecture 5A -- but it's messy!

Instead use indicator random variables to count something we do know the probability for: the probability of getting heads when flipping the coin once:

• For i = 1, 2, ... n define X_i = I{the ith flip results in event H}.
• Then X = ∑_i=1,nX_i.   (That is, count the flips individually and add them up.)
• Lemma 1 says that E[X_i] = Pr{H} = 1/2 for i = 1, 2, ... n.
• Expected number of heads is E[X] = E[∑_i=1,nX_i]
• Problem: We don't have ∑_i=1,nX_i; we only have E[X₁], E[X₂], ... E[X_n].
• Solution: Linearity of expectation (appendix C): expectation of sum equals sum of expectations. Therefore:
  

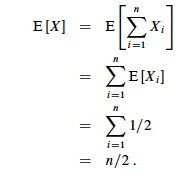
The key idea: if it's hard to count one way, use indicator random variables to count an easier way!

Hiring Problem Revisited

Assume that the candidates arrive in random order.

Let X be the random variable for the number of times we hire a new office assistant.

Define indicator random variables X₁, X₂, ... X_n where X_i = I{candidate i is hired}.

We will rely on these properties:

• X = X₁ + X₂ + ... + X_n   (The total number of hires is the sum of whether we did each individual hire (1) or not (0).)
• Lemma 1 implies that E[X_i] = Pr{candidate i is hired}.

We need to compute Pr{candidate i is hired}:

• Candidate i is hired iff candidate i is better than candidates 1, 2, ..., i−1
• Assumption of random order of arrival means any of the first i candidates are equally likely to be the best one so far.
• Thus, Pr{candidate i is the best so far} = 1/i.
  (Intuitively, as you add more candidates each candidate is less and less likely to be better than all the ones prior.)

By Lemma 1, E[X_i] = 1/i, a fact that lets us compute E[X]:

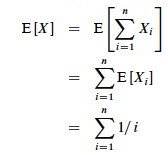
The sum is a harmonic series. From formula A7 in appendix A, the n^th harmonic number is:

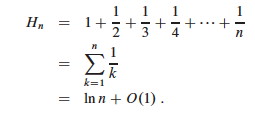
Thus, the expected hiring cost is O(c_h ln n), much better than worst case O(c_hn)! (ln is the natural log. Formula 3.15 of the text can be used to show that ln n = O(lg n.)

We will see this kind of analysis repeatedly. Its strengths are that it lets us count in ways for which we have probabilities (compare to C.37), and that it works even when there are dependencies between variables.

Randomized Algorithms

Above, we had to assume a distribution of inputs, but we may not have control over inputs.

An "adversary" can always mess up our assumptions by giving us worst case inputs. (This can be a fictional adversary in making analytic arguments, or it can be a real one ...)

Randomized algorithms foil the adversary by imposing a distribution of inputs.

The modifiation to HIRE-ASSISTANT is trivial: add a line at the beginning that randomizes the list of candidates.

• The randomization is now in the algorithm, not the input distribution.
• Whereas before the algorithm was deterministic, and we could predict the hiring cost for a given input, now we can no longer say what the hiring cost will be.
• But our payoff is that no particular input elicits worst-case behavior, even what was worst-case for the deterministic version!
• Bad behavior occurs only if we get "unlucky" numbers.

Having done so, the above analysis applies to give us expected value rather than average case.

What is the relationship/difference between probabilistic analysis and randomized algorithms?

Randomization Strategies

There are different ways to randomize algorithms. One way is to randomize the ordering of the input before we apply the original algorithm (as was suggested for HIRE-ASSISTANT above). A procedure for randomizing an array:

  Randomize-In-Place(A)
  1  n = A.length
  2  for i = 1 to n
  3      swap A[i] with A[Random(i,n)]  

The text offers a proof that this produces a uniform random permutation. It obviously runs in O(n) time.

Another approach to randomization is to randomize choices made within the algorithm.

Randomized Quicksort

We expect good average case behavior if all input permutations are equally likely, but what if it is not?

To get better performance on sorted or nearly sorted data -- and to foil our adversary! -- we can randomize the algorithm to get the same effect as if the input data were random.

Instead of explicitly permuting the input data (which is expensive), randomization can be accomplished trivially by random sampling of one of the array elements as the pivot.

If we swap the selected item with the last element, the existing PARTITION procedure applies:

Now, even an already sorted array will give us average behavior.

Curses! Foiled again!

Randomized Quicksort Analysis

The analysis assumes that all elements are unique, but with some work can be generalized to remove this assumption (Problem 7-2 in the text).

Worst Case

The previous analysis was pretty convincing, but was based on an assumption about the worst case. This analysis proves that our selection of the worst case was correct, and also shows something interesting: we can solve a recurrence relation with a "max" term in it!

PARTITION produces two subproblems, totaling size n-1. Suppose the partition takes place at index q. The recurrence for the worst case always selects the maximum cost among all possible ways of splitting the array (i.e., it always picks the worst possible q):

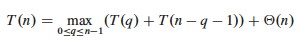
Based on the informal analysis, we guess T(n) ≤ cn² for some c. Substitute this guess into the recurrence:

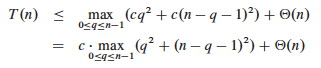
The maximum value of q² + (n - q - 1)² occurs when q is either 0 or n-1 (the second derivative is positive), and has value (n - 1)² in either case:

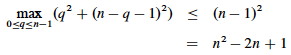
Substituting this back into the reucrrence:

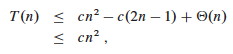
We can pick c so that c(2n - 1) dominates Θ(n). Therefore, the worst case running time is O(n²).

One can also show that the recurrence is Ω(n²), so worst case is Θ(n²).

Average (Expected) Case

With a randomized algorithm, expected case analysis is much more informative than worst-case analysis. Why?

This analysis nicely demonstrates the use of indicator variables and two useful strategies.

Setup

The dominant cost of the algorithm is partitioning. PARTITION removes the pivot element from future consideration, so is called at most n times.

QUICKSORT recurses on the partitions. The amount of work in each call is a constant plus the work done in the for loop. We can count the number of executions of the for loop by counting the number of comparisons performed in the loop.

Rather than counting the number of comparisons in each call to QUICKSORT, it is easier to derive a bound on the number of comparisons across the entire execution.

This is an example of a strategy that is often useful: if it is hard to count one way (e.g., "locally"), then count another way (e.g., "globally").

Let X be the total number of comparisons in all calls to PARTITION. The total work done over the entire execution is O(n + X), since QUICKSORT does constant work setting up n calls to PARTITION, and the work in PARTITION is proportional to X. But what is X?

Counting comparisons

For ease of analysis,

• Call the elements of A z₁, z₂, ... z_n, with z_i being the ith smallest element.
• Define the set Z_ij = {z_i, z_{i + 1}, ... z_j} to be the set of elements between z_i and z_j inclusive.

We want to count the number of comparisons. Each pair of elements is compared at most once, because elements are compared only to the pivot element and then the pivot element is never in any later call to PARTITION.

Indicator variables can be used to count the comparisons. (Recall that we are counting across all calls, not just during one partition.)

Let X_ij = I{ z_i is compared to z_j }

Since each pair is compared at most once, the total number of comparisons is:

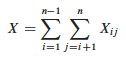
Taking the expectation of both sides, using linearity of expectation, and applying Lemma 5.1 (which relates expected values to probabilities):

Probability of comparisons

What's the probability of comparing z_i to z_j?

Here we apply another useful strategy: if it's hard to determine when something happens, think about when it does not happen.

Elements (keys) in separate partitions will not be compared. If we have done two comparisons among three elements and find that z_i < x <z_j, we do not need to compare z_i to z_j (no further information is gained), and QUICKSORT makes sure we do not by putting z_i and z_j in different partitions.

On the other hand, if either z_i or z_j is chosen as the pivot before any other element in Z_ij, then that element (as the pivot) will be compared to all of the elements of Z_ij except itself.

• The probability that z_i is compared to z_j is the probability that either is the first element chosen.
• Since there are j - i + 1 elements in Z_ij, and pivots are chosen randomly and independently, the probability that any one of them is chosen first is 1/(j - i + 1).

Therefore (using the fact that these are mutually exclusive events):

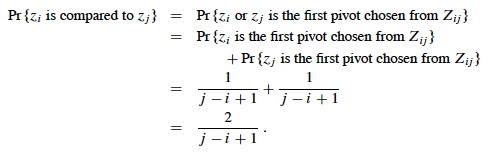
We can now substitute this probability into the analyis of E[X] above and continue it:

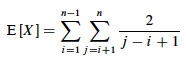
This is solved by applying equation A.7 for harmonic series, which we can match by substituting k = j - i and shifting the summation indices down i:

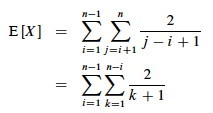
We can get rid of that pesky "+ 1" in the denominator by dropping it and switching to inequality (after all, this is an upper bound analysis), and now A7 (shown in box) applies:

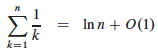
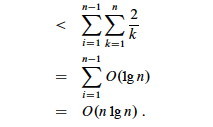
Above we used the fact that logs of different bases (e.g., ln n and lg n) grow the same asymptotically.

To recap, we started by noting that the total cost is O(n + X) where X is the number of comparisons, and we have just shown that X = O(n lg n).

Therefore, the average running time of QUICKSORT on uniformly distributed permutations (random data) and the expected running time of randomized QUICKSORT are both O(n + n lg n) = O(n lg n).

This is the same growth rate as merge sort and heap sort. Empirical studies show quicksort to be a very efficient sort in practice (better than the other n lg n sorts) whenever data is not already ordered. (When it is nearly ordered, such as only one item being out of order, insertion sort is a good choice.)

Expected Number of Inversions

Here is another example of probabilistic analysis. This is Exercise 5.2-5 page 122, for which there is a publicly posted solution. This example shows the great utility of random variables.

Let A[1.. n] be an array of n distinct numbers. If i < j and A[i] > A[j], then the pair (i, j) is called an inversion of A (they are "out of order" with respect to each other). Suppose that the elements of A form a uniform random permutation of ⟨1, 2, ... n⟩.

We want to find the expected number of inversions. This has obvious applications to analysis of sorting algorithms, as it is a measure of how much a sequence is "out of order". In fact, each iteration of the while loop in insertion sort corresponds to the elimination of one inversion (see the posted solution to problem 2-4c).

If we had to count in terms of whole permutations, figuring out how many permutations had 0 inversions, how many had 1, ... etc. (sound familiar? :), that would be a real pain, as there are n! permutations of n items. Can indicator random variables save us this pain by letting us count something easier?

We will count the number of inversions directly, without worrying about what permutations they occur in:

Let X_ij, i < j, be an indicator random variable for the event where A[i] > A[j] (they are inverted).

More precisely, define: X_ij= I{A[i] > A[j]} for 1 ≤ i < j ≤ n.

Pr{X_ij = 1} = 1/2 because given two distinct random numbers the probability that the first is bigger than the second is 1/2. (We don't care where they are in a permutation; just that we can easily identify the probabililty that they are out of order. Brilliant in its simplicity!)

By Lemma 1, E[X_ij] = 1/2, and now we are ready to count.

Let X be the random variable denoting the total number of inverted pairs in the array. X is the sum of all X_ij that meet the constraint 1 ≤ i < j ≤ n:

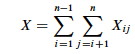
We want the expected number of inverted pairs, so take the expectation of both sides:

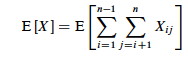
Using linearity of expectation, we can simplify this far:

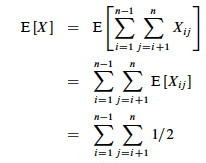
The fact that our nested summation is choosing 2 things out of n lets us write this as:

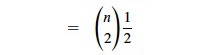
We can use formula C.2 from the appendix:

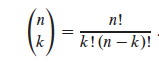
In screencast 5A I show how to simplify this to (n(n−1))/2, resulting in:

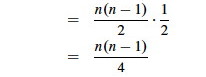
Therefore the expected number of inverted pairs is n(n − 1)/4, or O(n²).